Turbulence

• Model of Probability Distribution Functions (J. Eggers and Z. Jane Wang, Phys. Rev. E 57.4, 4281-4288 (1998) [PDF]) Motivated by my previous study of the helium turbulence, Jens Eggers and I conducted a quantitative study of the velocity differences measured by experimentalists. We have developed a model of the evolution of turbulence velocity differences from inertial scales to dissipative scales by taking into account the effects of viscosity. Our model suggests that the fluctuations of the viscous scales in turbulence produce a non-trivial crossover region in the velocity structure functions, which is generally neglected in data analysis. We show further that this crossover behavior is present in the experiments, which are analyzed in detail and compared with our model. We also discuss the importance of recognizing this crossover region when interpreting the experimental results. Assuming a finite and fixed spatial resolution, the model predicts a transition in the flatness at finite Reynolds number. We relate this observation with the reported transition.
• Helium Turbulence (Virginie Emsellem, Leo P. Kadanoff, Detlef Lohse, Patrick Tabeling, and Z. Jane Wang, Phys. Rev. E 55.3, 2672-2681 (1997) [PDF]) I collaborated with an experimental group at Ecole Normale Superieure in France (lead by Professor Tabeling) on a highly turbulent helium experiment. The experimentalists reported a novel transition at a very high Reynolds number, which is significant if confirmed. We analyzed their data to understand the origin of the transition and proposed two possible explanations related to the presence of the probe.
• Scaling and dissipation in the GOY shell model (Leo Kadanoff, Detlef Lohse, Jane Wang, and Roberto Benzi, Phys. of Fluids 7.3, 617-629 (1995) [PDF]) In this work on a cascade model of turbulence, we pointed out the existence of a helicity-like conserved quantity, in addition to the energy, and analyzed its significance in dynamical scalings. We further developed a better method of determining the scaling exponents than had been available. Our methods allowed us to analyze the connection between multifractality in the velocity distribution and in the dissipation at a given spatial scale. In addition, we predicted scaling behavior of temporal correlations of velocities, of the dissipation, and of Lyapunov indices.

Turbulent Diffusion and Random Non-Hermitian Matrices

• John Chalker and Z. Jane Wang, Spectrum of the Fokker-Planck operator representing diffusion in a random velocity field, Physical Review E, 61, 196 (2000) [PDF]
  

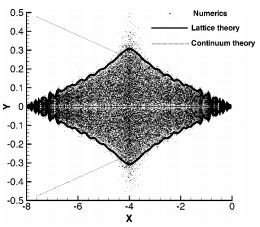
  We study spectral properties of the Fokker-Planck operator that represents particles moving via a combination of diffusion and advection in a time-independent random velocity field, presenting in detail work outlined elsewhere [J. T. Chalker and Z. J. Wang, Phys. Rev. Lett. 79, 1797 (1997)]. We calculate analytically the ensemble-averaged one-particle Green function and the eigenvalue density for this Fokker-Planck operator, using a diagrammatic expansion developed for resolvents of non-Hermitian random operators, together with a mean-field approximation ~the self-consistent Born approximation! which is well controlled in the weakdisorder regime for dimension d>2. The eigenvalue density in the complex plane is nonzero within a wedge that encloses the negative real axis. Particle motion is diffusive at long times, but for short times we find a novel time dependence of the mean-square displacement, <r^2>~t^(2/d) in dimension d>2, associated with the imaginary parts of eigenvalues.

• Spectral Theory of non-Hermitian Random Matrices and its Application to the Transport of Particles (J.T. Chalker and Z. Jane Wang, Phys. Rev. Lett. 79.10, 1797-1800 (1997) [PDF])
  

  I was interested in the spectral theory of non-Hermitian systems for two reasons: 1) analytical results on the spectral property of non-Hermitian systems were unknown and new techniques appear to be required, and 2) from the spectral property we can obtain time-dependent physically measurable quantities. For example, in the case of the Fokker-Planck operator, which describes the classic advection-diffusion problems, one can obtain from the spectra the time dependent diffusivity. John Chalker and I developed a general analytical technique using diagrammatic expansion to calculate the spectral properties of random non-Hermitian systems. By applying our technique to the diffusion-advection system, we discovered a novel scaling in effective diffusion at short times. The method also has broad applications to general non-Hermitian systems, such as the recently much discussed models of flux lines in superconductors.

• Localization of Particles in Fluids (Jonathan Miller and Jane Wang, Phys. Rev. Lett. 76.9, 1461-1464 (1996) [PDF]) We investigated the classic diffusion-advection problem using an approach different from previous analyses. In particular, we studied the connections between the scalings of passive scalars in fluids and localization problems in quantum disordered systems. We applied transfer matrix methods to both systems and showed that they exhibit universal features at a special point in the phase space, where divergent correlations are observed. Physically, this point corresponds to a long-range ordered phase emerging from chaotic background flows. We further suggested that similar critical behavior exists in a larger class of phenomena. Among these are "kinematic magnetic dynamos" by which magnetic fields are generated and sustained in stars.