Falling Parallelograms Physical Reviews E. 87 (2013) [PDF]
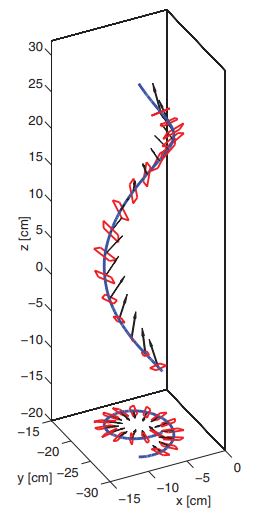
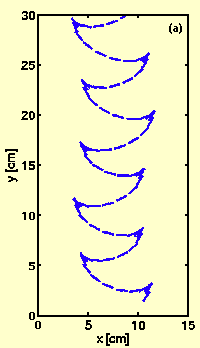
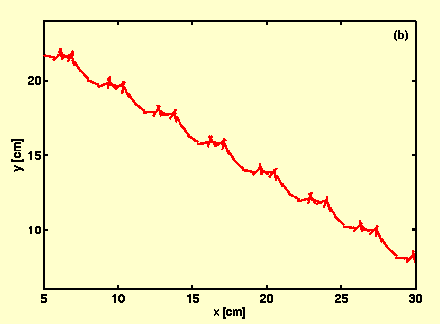
Falling parallelograms exhibit coupled motion of autogyration and tumbling, similar to the motion of falling tulip seeds, unlike maple seeds which autogyrate but do not tumble, or rectangular cards which tumble but do not gyrate. This coupled tumbling and autogyrating motion are robust, when card parameters, such as aspect ratio, internal angle, and mass density, are varied. We measure the three-dimensional (3D) falling kinematics of the parallelograms and quantify their descending speed, azimuthal rotation, tumbling rotation, and cone angle in each falling. The cone angle is insensitive to the variation of the card parameters, and the card tumbling axis does not overlap with but is close to the diagonal axis. In addition to this connection to the dynamics of falling seeds, these trajectories provide an ideal set of data to analyze 3D aerodynamic force and torque at an intermediate range of Reynolds numbers, and the results will be useful for constructing 3D aerodynamic force and torque models. Tracking these free falling trajectories gives us a nonintrusive method for deducing instantaneous aerodynamic forces. We determine the 3D aerodynamic forces and torques based on Newton-Euler equations. The dynamical analysis reveals that, although the angle of attack changes dramatically during tumbling, the aerodynamic forces have a weak dependence on the angle of attack. The aerodynamic lift is dominated by the coupling of translational and rotational velocities. The aerodynamic torque has an unexpectedly large component perpendicular to the card. The analysis of the Euler equation suggests that this large torque is related to the deviation of the tumbling axis from the principle axis of the card.
Maple Seed Nonlinearity. 25, C1-C8 (2012) [PDF]
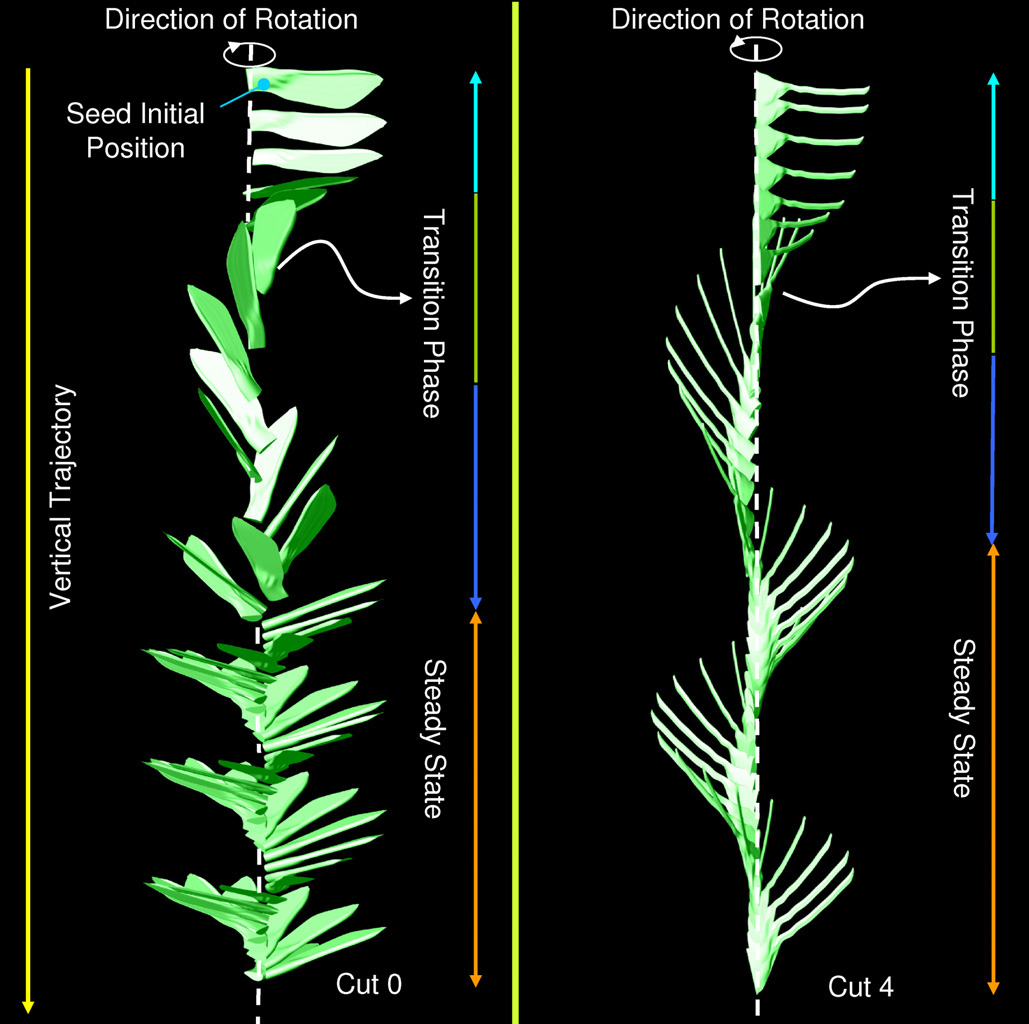
A maple seed falls in a characteristic helical motion. A crude analogy with autorotation of a wind turbine suggests that the torque due to the aerodynamic force would initiate the gyration of the seed. We were therefore surprised that a seed with a torn wing gyrates in a similar manner as a full-winged seed. In fact, a seed with only a sliver of leading edge can still gyrate. Thus the gyrating motion appears not to fully depend on the aerodynamic force. If, on the other hand, the aerodynamic force is completely absent, a seed would fall from rest like a rock in a vacuum.
To investigate how the seed reaches its steady helical motion, we use a high-speed digital camera to film the intact and cut seeds at 1000 Hz. With a mirror, the camera records two views simultaneously so that we can extract the 3D kinematics of the wing. We tracked the centre of mass and quantified the descending speed, the azimuthal rotation, and the cone angle for seeds with wings of different shapes. We found that the initial transition from rest to a steady gyration occurs in three steps: a tumble about the span-wise direction, followed by a tilt towards the vertical axis, leading to the gyration about the vertical axis and an opening of the cone angle before settling into a steady state. We offer a new explanation for the cause of the auto-gyration that accounts for these three stages.
Unsteady Aerodynamics of Fluttering and Tumbling Plates The Journal of Fluid Mechanics (2005) [PDF]
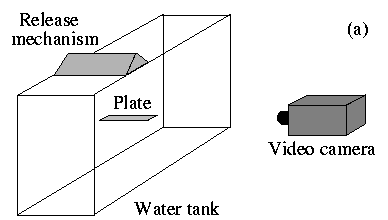

(a) experimental setup; (b) picture of release mechanism
In a table top experiment we have further investigated this type of dynamics and explored the two-dimensional trajectories of rigid metal plates falling in a water tank. Examples of the observed trajectories include periodic fluttering (side to side oscillations) and periodic tumbling (rotation and sideways drift). The measured trajectories give us the translational and the rotational plate acceleration, and since the plate dynamics is governed by gravity and fluid forces alone this permits us to extract the instantaneous fluid forces directly. Our model of the fluid forces with translational and rotational lift compares favorably with our experimental results for both fluttering and tumbling.
The vorticity plots shown below (with positive vorticity in red and negative vorticity in blue)are obtained by solving the two dimensional Navier-Stokes equations subject to the motion of free falling ellipses at Reynolds numbers around 10³. The Navier-Stokes equations are written in the vorticity-stream function formulation and solved efficiently via Fast Fourier Transform on a conformal grid.
The vortices in the wake of the tumbling ellipse (b) are either shed when the ellipse makes a 180° turn (the pair in the top left corner and the pair closest the ellipse) or generated when its wake becomes unstable (all other pairs). For computational reasons the flow around the fluttering ellipse (a) is at a lower Reynolds number (Re=400). In this case the wake instability has no time to develop and all the vortex pairs are generated at the turning point of its trajectory.
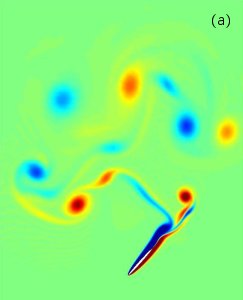

Vorticity diagrams: (a) fluttering; (b) tumbling
See movies of these calculations: fluttering (1.69Mb) and tumbling (2.11Mb). (Requires Quicktime or compatible player.)
Analysis of Transitions Between Fluttering, Tumbling and Steady Descent of Falling Cards The Journal of Fluid Mechanics (2005) [PDF]
In addition we have investigated the transition between periodic fluttering and periodic tumbling using the force model and direct numerical simulations. The dynamics depends on three non-dimensional numbers, the thickness to width ratio, the non-dimensional moment of inertia, and the Reynolds number. At intermediate Reynolds number we observe a transition between fluttering and tumbling with increasing non-dimensional moment of inertia, thereby confirming previous results which show that the value of the non-dimensional moment of inertia is crucial for predicting the effect of the aerodynamic coupling between the plate and the fluid. In the force model we find that the transition is a heteroclinic bifurcation which leads to a characteristic logarithmic divergence of the period of oscillation at the bifurcation point.
Falling Paper: Navier-Stokes Solutions, Model of Fluid Forces, and Center of Mass Elevation Physical Review Letters (2004) [PDF]

A piece of paper or a leaf flutters and tumbles down in a seemingly unpredictable manner, but it might give us some insight about flapping flight. A stumbling block in constructing a simple theory of freely falling objects is the quantitative description of the fluid force. Computationally and experimentally we have studied the dynamics of thin rigid objects falling freely in a fluid. A surprise came from the analysis of the fluid force. Our computations revealed that the circulation around a tumbling plate is proportional to the angular velocity, not to the translational velocity as in the case of a steadily translating plate.