Computational Fluid Dynamics and Vortex Dynamics
Description of Research
Immersed Interface Method
Sheng Xu is developing an immersed interface method to simulate flow with moving deformable complex boundaries, especially in biological fluid dynamics. The method will be applied to study the aerodynamics of insect flight with focus on the 3D and flexibility effects of insect wings.
In the immersed interface method, the boundaries are modeled as singular force in the Navier-Stokes equations. The construction of the singular force depends on whether the motions of the boundaries are prescribed or driven by force laws based on their deformation.
The numerical implementation of the method employs a fixed Cartesian grid for the flow and Lagrangian grids for the boudaries. The communication between the flow and the boundaries is achieved by incorporating into finite difference schemes the necessary jump conditions caused by the singular force and interpolating the velocity from the Cartesian grid to the Lagrangian grids. The necessary jump conditions have been systemtically derived in 3D (Xu and Wang, SIAM JSC, 2005[PDF]).
Results from a 2D implementation of the method show that: (1) second-order accuracy in the infinity norm for both the velocity and the pressure has been achieved; (2) computational cost is dominated by the pressure Poisson solver and the addition of a boundary introduces relatively insignificant cost; (3) the method is equally effective in computing flow subject to boundaries with prescribed forces or boundaries with prescribed motions.
Two 2D implementations (Xu and Wang, JCP, 2005[PDF]) are shown below. One shows the pressure field around five cylinders translating about a common center. The other shows a snapshot of the vorticity and the velocity fields induced by the relaxation of a distorted balloon. A 3D code has been developed and is under validation. A manuscript summarizing the 3D implementation and validation is to be submitted to J. Comp. Phys.
 |  | |
| pressure field around five cylinders translating about a common center | Vorticity fields induced by the relaxation of a distorted balloon |
Multiple-Wing Interaction: Computational Method
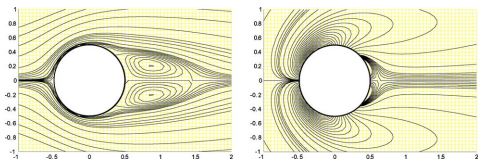
(D. Russell and ZJW, JCP 2003 [PDF]) To explore the possible benefit of multiple wing interactions, it is desirable to have an efficient computational tool to simulate multiple bodies moving in fluids. The existing methods involving grid regeneration or overset grids are intrinsically complicated. We developed a new algorithm for handing general fluid and solid body interactions, which is a two dimensional Cartesian grid method that treats the multiple objects as embedded discontinuities. The method uses O(N*ln(N)+M) per operation step, where N is the number of nodes in the regular Cartesian grid and M is the number of nodes in the immersed object surface discretization. The method is tested in the canonical examples of flow past cylinder and interactions of two cylinders, and now is being used to simulate flapping motions of dragonflies obtained in our recent experiments of tethered flight.
Far Field Boundary Conditions
(ZJW, JCP, 1999 [PDF]) Solving flows numerically in open geometry requires specification of flows at some finite computational boundary. I find a simple scheme for implementing the far-field boundary condition exactly for the Poisson equation with source term of finite support. This numerical scheme avoids introducing mixed boundary conditions in the far field, thus it can be used efficiently with FFT.
Vortex Dynamics
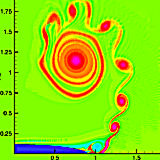
Secondary Shear Instabilities (Z. Jane Wang, J.G. Liu, and S. Childress, Phys. of Fluids, 11.9, 2446-2448 (1999) [PDF]) We investigate shear instabilities leading to secondary vortices in flow past an ellipse at high Reynolds numbers (Re=10^4) by direct numerical simulation. We find that the temporal and spatial periodicities in the shear layer are independent of the numerical resolutions. More interestingly, the turnover time of the corner vortex coincides with the periodicity of the vortex roll-up in the shear layer. We hypothesize that the corner vortex acts as a rotor for triggering the instabilities.
Publications
- Sheng Xu and Z. Jane Wang, Systematic Derivation of Jump Conditions for the Immersed Interface Method in Three-dimensional Flow Simulation, SIAM J. Sci. Comp. 27.6, 1948-1980 (2006) [PDF]
- Sheng Xu and Z. Jane Wang, An Immersed Interface Method for Simulating the Interaction of a Fluid with Moving Boundaries, J. Comp. Phys 201, 454-493 (2006) [PDF]
- David Russell and Z. Jane Wang, A cartesian grid method for modeling multiple moving objects in 2D incompressible viscous flow, J. Comp. Phys. 191, 177-205 (2003) [PDF]
- Z. Jane Wang, Efficient Implementation of the Exact Numerical Far field Boundary Condition for Poisson Equation on an Infinite Domain, J. Comp. Phys. 153, 666 (1999) [PDF]
- Z. Jane Wang, J.G. Liu, and S. Childress, Connection between corner vortices and shear layer instability in flow past an ellipse, Phys. of Fluids 11.9, 2446-2448 (1999) [PDF]