Reviews
- Z. Jane Wang, Insect Flight: From Newton's Law to Neurons , Annual Review of Condensed Matter Physics, 2016 [PDF]
- Z. Jane Wang, Insect Flight , Princeton Companion to Applied Mathematics, 2015
- Z. Jane Wang, Dragonfly Flight, Physics Today, October (2008) [PDF]
- Z. Jane Wang, Dissecting Insect Flight, Annu. Rev. Fluid Mech. 35.37, 183-210 (2005) [PDF]
Optimal wing hinge location for fast ascent in a model fly Journal of Fluid Mechanics (2018) [PDF]
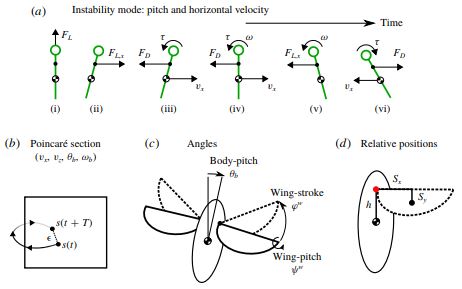
It was thought that the wing hinge position can be tuned to stabilize an uncontrolled fly. However here, our Floquet stability analysis shows that the hinge position has a weak dependence on the flight stability. As long as the hinge position is within the fly's body length, both hovering and ascending flight are unstable. Instead, there is an optimal hinge position, h*, at which the ascending speed is maximized. h* is approximately half way between the centre of mass and the top of the body. We show that the optimal h* is associated with the anti-resonance of the body-wing coupling, and is independent of the stroke amplitude. At h*, the torque due to wing inertia nearly cancels the torque due to aerodynamic lift, minimizing the body oscillation thus maximizing the upward force. Our analysis using a simplified model of two coupled masses further predicts, h* = (mt/mw)(g/ω2). These results suggest that the ascending speed, in addition to energetics and stability, is a trait that insects are likely to optimize.
Predicting fruit fly's sensing rate with insect flight simulations Proceedings of the National Academy of Sciences (2014) [PDF]
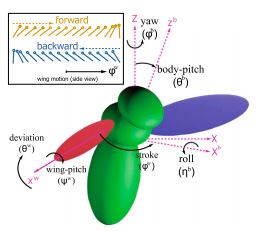
Without sensory feedback, flies cannot fly. Exactly how various feedback controls work in insects is a complex puzzle to solve. What do insects measure to stabilize their flight? How often and how fast must insects adjust their wings to remain stable? To gain insights into algorithms used by insects to control their dynamic instability, we develop a simulation tool to study free flight. To stabilize flight, we construct a control algorithm that modulates wing motion based on discrete measurements of the body-pitch orientation. Our simulations give theoretical bounds on both the sensing rate and the delay time between sensing and actuation. Interpreting our findings together with experimental results on fruit flies' reaction time and sensory motor reflexes, we conjecture that fruit flies sense their kinematic states every wing beat to stabilize their flight. We further propose a candidate for such a control involving the fly's haltere and first basalar motor neuron. Although we focus on fruit flies as a case study, the framework for our simulation and discrete control algorithms is applicable to studies of both natural and man-made fliers.
Active and passive stabilization of body pitch in insect flight Journal of the Royal Society Interface (2013) [PDF]
Flying insects have evolved sophisticated sensory–motor systems, and here we argue that such systems are used to keep upright against intrinsic flight instabilities. We describe a theory that predicts the instability growth rate in body pitch from flapping-wing aerodynamics and reveals two ways of achieving balanced flight: active control with sufficiently rapid reactions and passive stabilization with high body drag. By glueing magnets to fruit flies and perturbing their flight using magnetic impulses, we show that these insects employ active control that is indeed fast relative to the instability. Moreover, we find that fruit flies with their control sensors disabled can keep upright if high-drag fibres are also attached to their bodies, an observation consistent with our prediction for the passive stability condition. Finally, we extend this framework to unify the control strategies used by hovering animals and also furnish criteria for achieving pitch stability in flapping-wing robots.
Paddling Mode of Forward Flight in Insects Physical Review Letters (2011) [PDF]

By analyzing high-speed video of the fruit fly, we discover a swimminglike mode of forward flight characterized by paddling wing motions. We develop a new aerodynamic analysis procedure to show that these insects generate drag-based thrust by slicing their wings forward at low angle of attack and pushing backwards at a higher angle. Reduced-order models and simulations reveal that the law for flight speed is determined by these wing motions but is insensitive to material properties of the fluids. Thus, paddling is as effective in air as in water and represents a common strategy for propulsion through aquatic and aerial environments.
Turning Maneuver in Free Flight Physical Review Letters (2010) [PDF]

Flying insects execute aerial maneuvers through subtle manipulations of their wing motions. Here, we measure the free-flight kinematics of fruit flies and determine how they modulate their wing pitching to induce sharp turns. By analyzing the torques these insects exert to pitch their wings, we infer that the wing hinge acts as a torsional spring that passively resists the wing's tendency to flip in response to aerodynamic and inertial forces. To turn, the insects asymmetrically change the spring rest angles to generate asymmetric rowing motions of their wings. Thus, insects can generate these maneuvers using only a slight active actuation that biases their wing motion.
Discovering the Flight Autostabilizer of Fruitflies by Inducing Aerial Stumbles Proceedings of the National Academy of Sciences (2010) [PDF]

Just as the Wright brothers implemented controls to achieve stable airplane flight, flying insects have evolved behavioral strategies that ensure recovery from flight disturbances. Pioneering studies performed on tethered and dissected insects demonstrate that the sensory, neurological, and musculoskeletal systems play important roles in flight control. Such studies, however, cannot produce an integrative model of insect flight stability because they do not incorporate the interaction of these systems with free-flight aerodynamics. We directly investigate control and stability through the application of torque impulses to freely flying fruit flies (Drosophila melanogaster) and measurement of their behavioral response. High-speed video and a new motion tracking method capture the aerial "stumble," and we discover that flies respond to gentle disturbances by accurately returning to their original orientation. These insects take advantage of a stabilizing aerodynamic influence and active torque generation to recover their heading to within 2° in <60 ms. To explain this recovery behavior, we form a feedback control model that includes the fly's ability to sense body rotations, process this information, and actuate the wing motions that generate corrective aerodynamic torque. Thus, like early man-made aircraft and modern fighter jets, the fruit fly employs an automatic stabilization scheme that reacts to short time-scale disturbances.
3D Tracking of Insects in Free Flight The Journal of Experimental Biology (2009) [PDF]
Flying insects perform complex aerial maneuvers via slight manipulation of their wing motion. In order to capture these subtle kinematics, it is primordial to use a method that enables us to discern between consistent flight strategies used by the insect from inconsistent variations and measurement errors. Accordingly, we introduce a novel automated method that accurately extracts full 3D body and wing kinematics from high-resolution films of free-flying insects. Thsi method combines visual hull reconstruction, principal component analysis (PCA), and geometric information about the insect to recover times series data of positions and orientations.
Efficiency of Flapping vs. Fixed Wings Flight The Journal of Experimental Biology (2008) [PDF] | Physical Review Letters (2009) [PDF]

Flapping Flight is more maneuverable than steady flight. It is debated whether this advantage is necessarily accompanied by a trade-off in the flight efficiency. This leads us to ask if there exists any flapping motion that is aerodynamically more efficient than the optimal steady motion. We solve the 2D Navier Stokes equations around a flapping airfoil and determine the minimal aerodynamic power required to support a specific weight. Although most flapping wings are more costly than the optimal steady wing motion, we find that optimized flapping wing motions can save up to 27% of the aerodynamic power required by the optimal steady flight.
Passive Motions in Insect Flight The Journal of Fluid Mechanics (2007) [PDF]

Wing pitch reversal is the rapid change of angle of attack near stroke transition. This motion represents one of the most significant differences between hovering with flapping wings and with a continuously rotating blade (e.g. helicopter flight). We found the surprising fact that, eventhough insects have the musculature to control this motion, aerodynamic and wing inertia forces are sufficient to pitch the wing without the aid of the muscles.
Energy Minimization in Insect Flight The Journal of Fluid Mechanics (2007) [PDF]

Insect flight is a metabolically costly endeavor which requires mass-specific oxygen consumption rates of an order of magnitude higher than those measured in terrestrial insects. Hovering is particular costly since there is no ambient wind to help in lift generation. In this study, we test the hypothesis according to which insects move their wings in a way to minimize the metabolic cost associated with their motion.
Fore and Hind Wing Interactions of Dragonfly Flight Physical Review Letters (2007) [PDF]
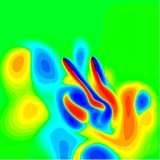
A distinctive feature of dragonflies is their use of two pairs of wings instead of one pair. This reflects their ancient origin. As such, understanding the coupling between their fore and hind wings might shed light on the evolution of flight based on four wings to that based on two. We are tackling this problem on two fronts. The first is to develop a computational tool to simulate flows around multiple bodies in relative motion. The second involves an experiment on tethered dragonflies in which we measure the 3D wing kinematics and vertical forces. The kinematics is an input to our computation and we are analyzing the forces due to wing coupling.
Erratic Trajectory of Butterfly Flight

Some butterflies appear to fly crooked, lurching here and there. Their close relatives, moths, however appear to fly relatively straight. Why? We have filmed free butterfly flight under different conditions and extracted their 3D trajectories. Currently we are analyzing the data in the hopes of figuring out a correlation between their flight behavior and wing geometry.
The Role of Drag in Hovering and Lessons About Hovering Efficiency The Journal of Experimental Biology (2004) [PDF]
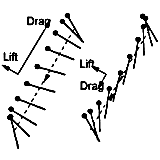
Airplanes and helicopters are airborne via aerodynamic lift, not drag. However, it is not a priori clear that insects use only lift to fly. A dragonfly uses mostly drag to hover by employing asymmetric up and down strokes along an inclined stroke plane. But is it efficient to use drag? Our computations of a family of strokes, which use various combination of lift and drag to produce the net vertical force, show that using drag can be as efficient as using lift. This finding further lead us to construct a simple example in which hovering efficiency can be improved two-fold when using both lift and drag, compared to using lift alone.
Comparing Against Experiments The Journal of Experimental Biology (2004) [PDF]
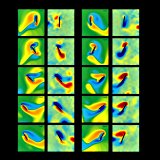
We compare two dimensional computations against the robotic fruitfly experiments. In particular, we investigate unsteady effects and the degree of agreement between two dimensional computations and three dimensional experiments in several qualitatively different flows. Analysis of the success and failure of a two dimensional model in capturing the forces and flows in three dimensional experiments provides new insight about the role of three dimensional effects in flapping flight, for example, the relevance of the axial flow in dynamic stall.
Unsteady Forces on an Accelerating Plate The Journal of Fluid Mechanics (2004) [PDF]
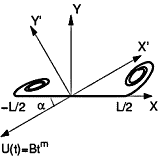
The vortical flow seen in simulation of hovering flight suggested a need for better understanding of separated flow behind a plate, but there have been limited theoretical tools. To fill this gap, we study the aerodynamic forces on a flat plate accelerating from rest at fixed incidence in two-dimensional power-law flow analytically and numerically. An inviscid approximation is made in which separation at the two plate edges is modeled by growing spiral vortex sheets, whose evolution is determined by the Birkhoff-Rott equation, and solved with a similarity expansion. This gives a mechanism for dynamic stall based on a combination of unsteady vortex lift and pure added mass; the incidence angle for maximum vortex lift is arccos[sqrt(3/8)] or approximately 52.2° independent of the acceleration profile. Circulation on the flat plate makes no direct contribution. Both lift and drag force predictions from the unsteady inviscid theory are compared with those obtained from numerical solutions of the two-dimensional unsteady Navier Stokes equations for an ellipse of high aspect ratio, and with predictions of Wagner's classical theory. Estimates for the shed circulation and the size of the start-up vortices are also obtained.
Hovering Dragonfly Flight Physical Review Letters (2000) [PDF]

Hovering is an extreme mode of flight where the forward velocity is zero. To do this, insects must draw clean air from the ambient flow and get rid of the `messy vortices' they have created to obtain a large periodic lift. Solutions to the two dimensional Navier Stokes equation around generic hovering wing undergoing motions similar to dragonfly flight revealed a process by which a downward jet of pairs of counter-rotating vortices is created. The momentum carried down by the dipoles provides enough lift to support a typical insect's weight. This two dimensional mechanism of lift generation has a natural extension in three dimensions, where the pairs of vortices are replaced by vortex rings.
Forward Flight The Journal of Fluid Mechanics (2000) [PDF]
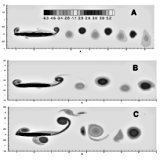
Frequency variation among different species is one of the distinctive features of insect flight. However, classical quasi-steady analysis does not predict a preferred frequency.Computations of a minimal model of forward flapping motion shows an unsteady mechanism for selecting a preferred range of flapping frequency for a given size of wing. The frequency range is dictated by the time scales associated with the growth of the trailing and leading edge vortices. The predicted inverse scaling between the frequency and the length of the wing is consistent with the zoological data available for birds and insects over almost three orders of magnitude in wing length.

Just as the Wright brothers implemented controls to achieve stable airplane flight, flying insects have evolved behavioral strategies that ensure recovery from flight disturbances. Pioneering studies performed on tethered and dissected insects demonstrate that the sensory, neurological, and musculoskeletal systems play important roles in flight control. Such studies, however, cannot produce an integrative model of insect flight stability because they do not incorporate the interaction of these systems with free-flight aerodynamics. We directly investigate control and stability through the application of torque impulses to freely flying fruit flies (Drosophila melanogaster) and measurement of their behavioral response. High-speed video and a new motion tracking method capture the aerial "stumble," and we discover that flies respond to gentle disturbances by accurately returning to their original orientation. These insects take advantage of a stabilizing aerodynamic influence and active torque generation to recover their heading to within 2° in <60 ms. To explain this recovery behavior, we form a feedback control model that includes the fly's ability to sense body rotations, process this information, and actuate the wing motions that generate corrective aerodynamic torque. Thus, like early man-made aircraft and modern fighter jets, the fruit fly employs an automatic stabilization scheme that reacts to short time-scale disturbances.

Flying insects perform complex aerial maneuvers via slight manipulation of their wing motion. In order to capture these subtle kinematics, it is primordial to use a method that enables us to discern between consistent flight strategies used by the insect from inconsistent variations and measurement errors. Accordingly, we introduce a novel automated method that accurately extracts full 3D body and wing kinematics from high-resolution films of free-flying insects. Thsi method combines visual hull reconstruction, principal component analysis (PCA), and geometric information about the insect to recover times series data of positions and orientations.

Flapping Flight is more maneuverable than steady flight. It is debated whether this advantage is necessarily accompanied by a trade-off in the flight efficiency. This leads us to ask if there exists any flapping motion that is aerodynamically more efficient than the optimal steady motion. We solve the 2D Navier Stokes equations around a flapping airfoil and determine the minimal aerodynamic power required to support a specific weight. Although most flapping wings are more costly than the optimal steady wing motion, we find that optimized flapping wing motions can save up to 27% of the aerodynamic power required by the optimal steady flight.

Wing pitch reversal is the rapid change of angle of attack near stroke transition. This motion represents one of the most significant differences between hovering with flapping wings and with a continuously rotating blade (e.g. helicopter flight). We found the surprising fact that, eventhough insects have the musculature to control this motion, aerodynamic and wing inertia forces are sufficient to pitch the wing without the aid of the muscles.

Insect flight is a metabolically costly endeavor which requires mass-specific oxygen consumption rates of an order of magnitude higher than those measured in terrestrial insects. Hovering is particular costly since there is no ambient wind to help in lift generation. In this study, we test the hypothesis according to which insects move their wings in a way to minimize the metabolic cost associated with their motion.

A distinctive feature of dragonflies is their use of two pairs of wings instead of one pair. This reflects their ancient origin. As such, understanding the coupling between their fore and hind wings might shed light on the evolution of flight based on four wings to that based on two. We are tackling this problem on two fronts. The first is to develop a computational tool to simulate flows around multiple bodies in relative motion. The second involves an experiment on tethered dragonflies in which we measure the 3D wing kinematics and vertical forces. The kinematics is an input to our computation and we are analyzing the forces due to wing coupling.

Some butterflies appear to fly crooked, lurching here and there. Their close relatives, moths, however appear to fly relatively straight. Why? We have filmed free butterfly flight under different conditions and extracted their 3D trajectories. Currently we are analyzing the data in the hopes of figuring out a correlation between their flight behavior and wing geometry.

Airplanes and helicopters are airborne via aerodynamic lift, not drag. However, it is not a priori clear that insects use only lift to fly. A dragonfly uses mostly drag to hover by employing asymmetric up and down strokes along an inclined stroke plane. But is it efficient to use drag? Our computations of a family of strokes, which use various combination of lift and drag to produce the net vertical force, show that using drag can be as efficient as using lift. This finding further lead us to construct a simple example in which hovering efficiency can be improved two-fold when using both lift and drag, compared to using lift alone.

We compare two dimensional computations against the robotic fruitfly experiments. In particular, we investigate unsteady effects and the degree of agreement between two dimensional computations and three dimensional experiments in several qualitatively different flows. Analysis of the success and failure of a two dimensional model in capturing the forces and flows in three dimensional experiments provides new insight about the role of three dimensional effects in flapping flight, for example, the relevance of the axial flow in dynamic stall.

The vortical flow seen in simulation of hovering flight suggested a need for better understanding of separated flow behind a plate, but there have been limited theoretical tools. To fill this gap, we study the aerodynamic forces on a flat plate accelerating from rest at fixed incidence in two-dimensional power-law flow analytically and numerically. An inviscid approximation is made in which separation at the two plate edges is modeled by growing spiral vortex sheets, whose evolution is determined by the Birkhoff-Rott equation, and solved with a similarity expansion. This gives a mechanism for dynamic stall based on a combination of unsteady vortex lift and pure added mass; the incidence angle for maximum vortex lift is arccos[sqrt(3/8)] or approximately 52.2° independent of the acceleration profile. Circulation on the flat plate makes no direct contribution. Both lift and drag force predictions from the unsteady inviscid theory are compared with those obtained from numerical solutions of the two-dimensional unsteady Navier Stokes equations for an ellipse of high aspect ratio, and with predictions of Wagner's classical theory. Estimates for the shed circulation and the size of the start-up vortices are also obtained.

Hovering is an extreme mode of flight where the forward velocity is zero. To do this, insects must draw clean air from the ambient flow and get rid of the `messy vortices' they have created to obtain a large periodic lift. Solutions to the two dimensional Navier Stokes equation around generic hovering wing undergoing motions similar to dragonfly flight revealed a process by which a downward jet of pairs of counter-rotating vortices is created. The momentum carried down by the dipoles provides enough lift to support a typical insect's weight. This two dimensional mechanism of lift generation has a natural extension in three dimensions, where the pairs of vortices are replaced by vortex rings.

Frequency variation among different species is one of the distinctive features of insect flight. However, classical quasi-steady analysis does not predict a preferred frequency.Computations of a minimal model of forward flapping motion shows an unsteady mechanism for selecting a preferred range of flapping frequency for a given size of wing. The frequency range is dictated by the time scales associated with the growth of the trailing and leading edge vortices. The predicted inverse scaling between the frequency and the length of the wing is consistent with the zoological data available for birds and insects over almost three orders of magnitude in wing length.